Eric Forgy Notes on Grothendieck Topologies, Fibered Categories and Descent Theory
This pages represents notes to myself (anyone is more than welcome to comment) as I attempt to read through Chapter 2 of
- Vistoli, Notes on Grothendieck topologies, fibered categories and descent theory (pdf)
I like to draw pictures to help me understand things, so as I go through the paper, I will try to draw some illustration for the main concepts.
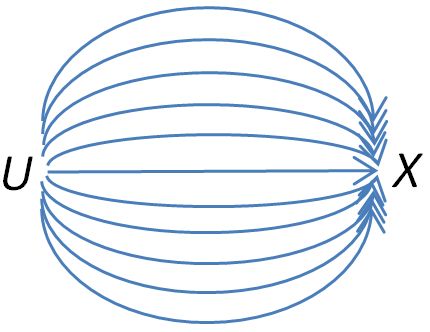
The set of morphisms in a category between objects and will be depicted by a ball of “strands”, i.e. morphisms stretching between the two objects.
Instead of calling a functor , I’d like to see how far I can get by calling it a contravariant functor instead. Contravariant functors seem more intuitive to me than opposite categories.
This contravariant functor sends the object to the set of morphisms as illustrated below.

A morphism in gets sent to the function in the opposite direction in .
To see this, note that the morphism effectively pulls (“combs”) the strands in back to strands in (kind of like a “ponytail”) via
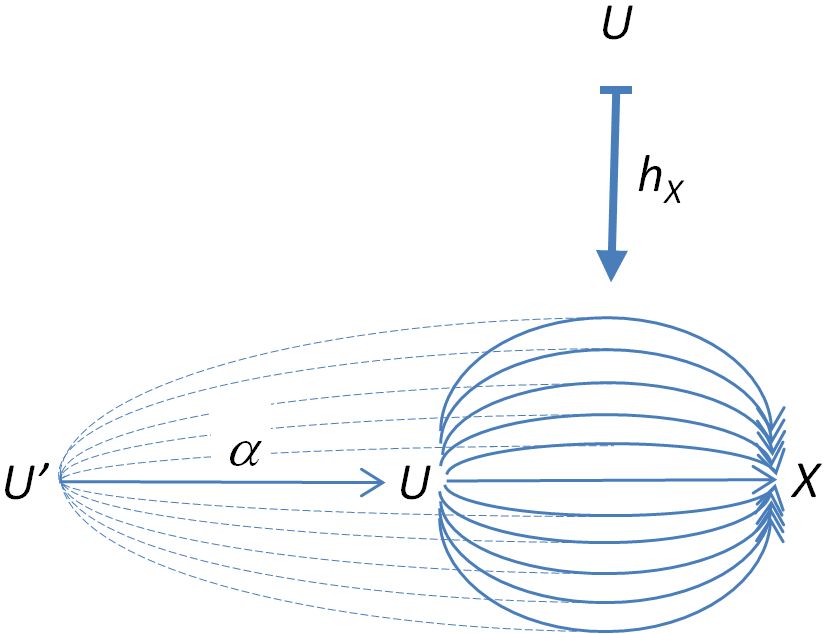
A morphism in induces a natural transformation
To see this, note the morphism effectively pushes (“combs”) the strands in forward to strands in via
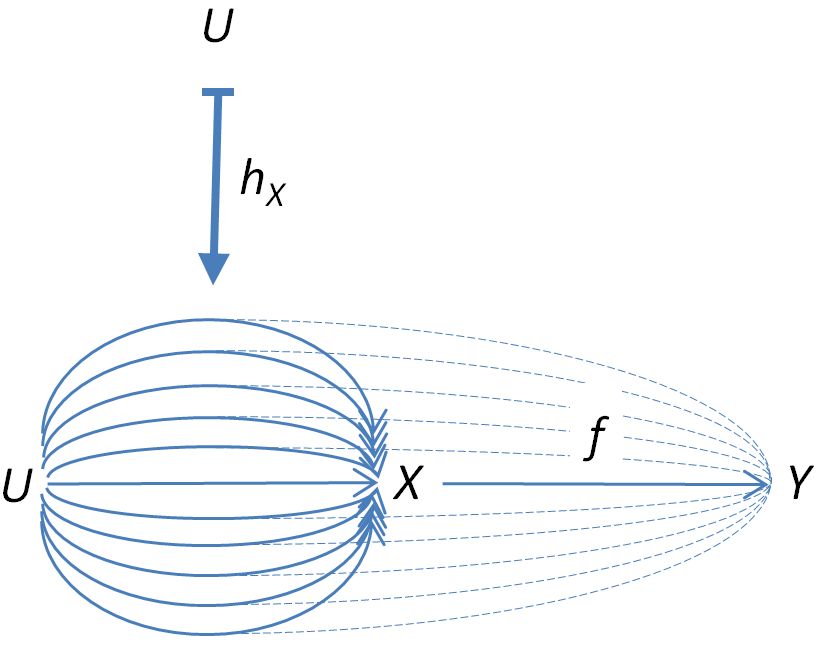
For this to be a natural transformation, we need to have the commuting diagram
but this simply means that it doesn’t matter if we first “comb” the strands back to and then comb the strands forward to , or comb the strands forward to first and then comb the strands back to
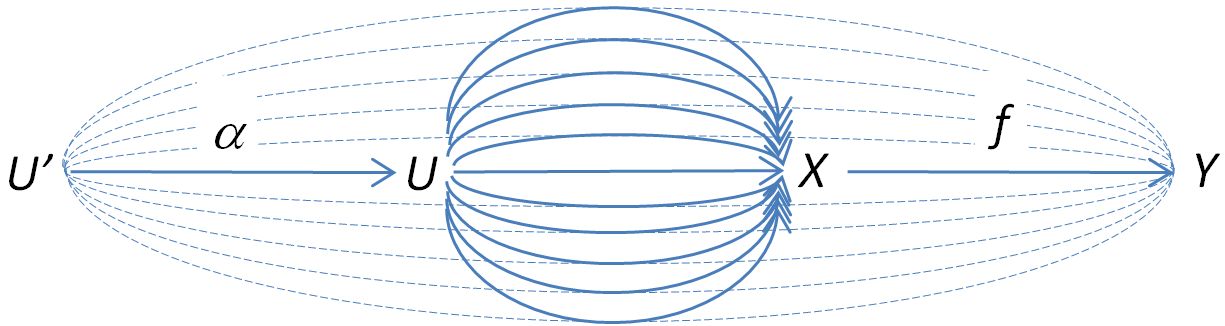
which follows from associativity of morphisms in .